贝塞尔曲线原理及实现

贝塞尔曲线于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由 Paul de Casteljau 于1959年运用 de Casteljau 算法开发，以稳定数值的方法求出贝塞尔曲线。

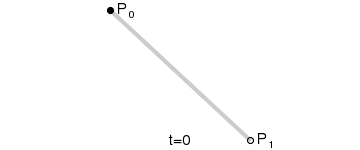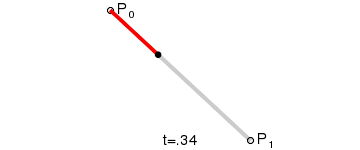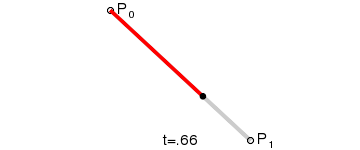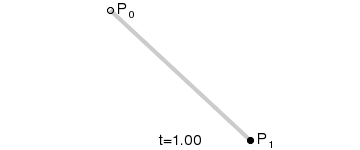
1.线性贝塞尔曲线

P(t)=(1-t)P₀+tP₁ , 0<=t<=1;

2.二次贝塞尔曲线

P(t)=(1-t)²P₀+2t(1-t)P₁+t²P₂ ,0<=t<=1;

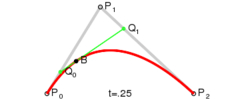
P₀Q₀:P₀P₁=P₁Q₁:P₁P₂=Q₀B:Q₀Q₁

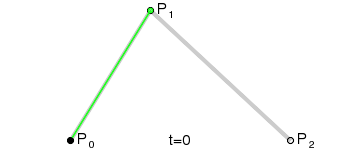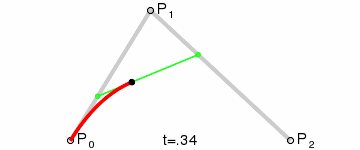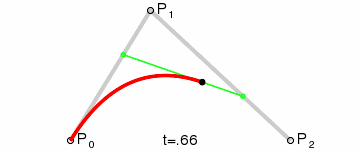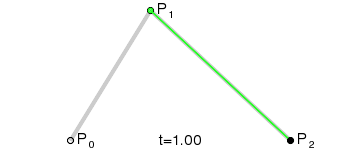
3.三次贝塞尔曲线

P(t)=(1-t)³P₀+3t(1-t)²P₁+3t²(1-t)P₂+t³P₃  ,0<=t<=1;

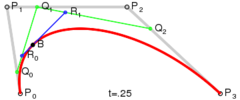
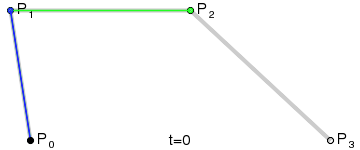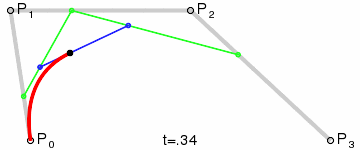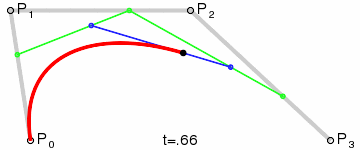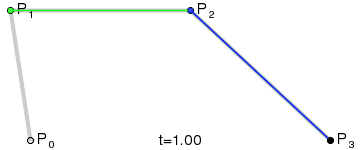
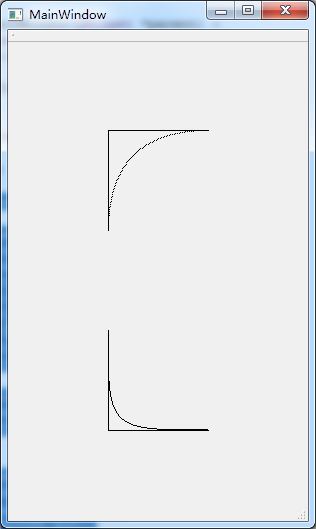
二次贝塞尔曲线的实现：

• 法一：由函数求出对应点，描点画线；
• 法二：Qt cubicTo()画线；

void MainWindow::paintEvent(QPaintEvent *)
{
    QPainter painter(this);
    painter.drawLine(100,100,100,200);
    painter.drawLine(100,100,200,100);
    QPointF p0(100,200);
    QPointF p1(100,100);
    QPointF p2(200,100);
    QPointF d;
    double i=0;//方法一
    while(i<=1)
    {
        d=(1-i)*(1-i)*p0+2*i*(1-i)*p1+i*i*p2;
        painter.drawPoint(d);
        i+=0.01;
    }

    painter.drawLine(100,300,100,400);
    painter.drawLine(100,400,200,400);
    QPainterPath path;//方法二
    path.moveTo(100,300);
    path.cubicTo(100,400,100,400,200,400);
    painter.drawPath(path);
}